Выпуклые функции (convex function) достаточно просты, поскольку имеют только один локальный минимум. Невыпуклые функции (non-convex function) могут быть намного сложнее. В этой статье мы рассмотрим различные типы критических точек, которые могут встретиться при работе с невыпуклыми функциями. В частности, мы увидим, что во многих случаях простой эвристический подход на основе градиентного спуска (gradient descent) позволяет достичь локального минимума за полиномиальное время.
Различные типы критических точек
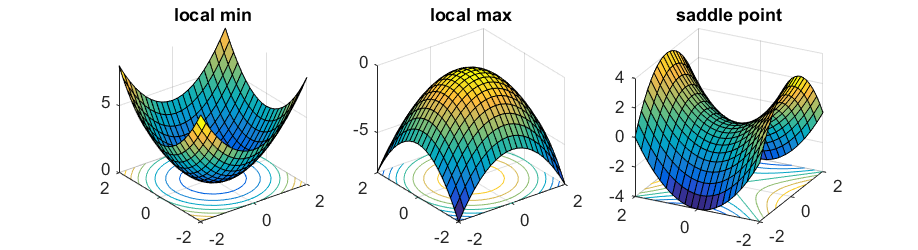
local min – локальный минимум local max – локальный максимум saddle point – седловая точка
Согласно наиболее популярному методу, чтобы минимизировать функцию [latex]f:\mathbb{R}^n\to \mathbb{R}[/latex], необходимо двигаться в направлении противоположном градиенту [latex]\nabla f(x)[/latex] (для простоты все функции, о которых идет речь, мы будем считать бесконечно дифференцируемыми):
[latex]y = x — \eta \nabla f(x)[/latex]
Здесь [latex]\eta[/latex] – малый шаг. Это и есть алгоритм градиентного спуска.
Если градиент [latex]\nabla f(x)[/latex] отличен от нуля, и мы выбираем достаточно малое значение [latex]\eta[/latex], алгоритм будет гарантированно локально прогрессировать. Если же градиент [latex]\nabla f(x)[/latex] равен [latex]\vec{0}[/latex], значит, мы достигли критической точки, в которой алгоритм градиентного спуска остановится. Для (сильно) выпуклой функции эта критическая точка является единственной и представляет собой глобальный минимум.
Однако в случае невыпуклой функции равенство градиента нулю еще не говорит об успехе. Хорошим примером является следующая функция:
[latex]y = x_1^2 — x_2^2.[/latex]
В точке [latex]x = (0,0)[/latex] градиент равен [latex]\vec{0}[/latex], однако очевидно, что эта точка не является локальным минимумом, поскольку при [latex]x = (0, \epsilon)[/latex] функция имеет меньшее значение. Точка [latex](0,0)[/latex] называется седловой точкой (saddle point) данной функции.
Чтобы различать описанные выше случаи, необходимо рассмотреть производную второго порядка [latex]\nabla^2 f(x)[/latex], то есть матрицу [latex]n\times n[/latex], называемую гессианом (Hessian), [latex]i,j[/latex]-элементы которой вычисляются следующим образом: [latex]\frac{\partial^2}{\partial x_i \partial x_j} f(x)[/latex]. Если гессиан является положительно определенным (то есть [latex]u^\top\nabla^2 f(x) u > 0[/latex] для любого [latex]u\ne 0[/latex]) посредством разложения в ряд Тейлора второго порядка для любого направления [latex]u[/latex] [latex]f(x + \eta u) \approx f(x) + \frac{\eta^2}{2} u^\top\nabla^2 f(x) u > f(x)[/latex], тогда [latex]x[/latex] является локальным минимумом. Аналогично, если гессиан является отрицательно определенным, – точка представляет собой локальный максимум. Если же гессиан имеет как положительные, так и отрицательные собственные значения (eigenvalue), – точка является седловой.
Считается, что для многих задач, включая обучение глубоких сетей, почти все локальные минимумы имеют значения функции близкие к глобальному оптимуму. Следовательно, для решения таких задач достаточно найти локальный минимум. Однако даже поиск локального минимума является NP-трудным (см. обсуждение в работе [Anandkumar, Ge]). Многие популярные методы оптимизации на практике являются алгоритмами оптимизации первого порядка, то есть используют лишь градиент, не вычисляя при этом гессиан в явном виде. Следовательно, подобные алгоритмы не могут преодолевать седловые точки.
Далее мы увидим, что «застревание» алгоритма в седловой точке является очень вероятным сценарием, поскольку большинство естественных целевых функций имеет экспоненциально большое количество таких точек. Затем мы обсудим, каким образом алгоритм может выбраться из седловой точки.
Симметрия и седловые точки
Многие задачи машинного обучения можно абстрагировать, как поиск k различных компонент (иногда называемых признаками (feature), центрами (center) и т.д.). Например, в задаче кластеризации (clustering) мы имеем n точек и ищем k компонент, минимизирующих сумму расстояний от точек до ближайших центров. В случае двухслойной нейронной сети мы ищем сеть, содержащую k различных нейронов в среднем слое. В задаче разложения тензора (tensor decomposition) также выполняется поиск k различных компонент на единицу меньшего ранга.
Распространенным способом решения таких задач является применение целевой функции: пусть [latex]x_1, x_2, \ldots, x_k \in \mathbb{R}^n[/latex] обозначают центры, и пусть целевая функция [latex]f(x_1, \ldots, x_k)[/latex] оценивает качество решения. Целевая функция достигает минимума, когда векторы [latex]x_1, x_2, \ldots, x_k[/latex] являются искомыми [latex]k[/latex] компонентами.
Естественная причина, в результате которой любая подобная задача по своей сути является невыпуклой, заключается в симметрии перестановок (permutation symmetry). Например, если поменять местами первую и вторую компоненту, решения будут эквивалентны: [latex]f(x_1, x_2, \ldots, x_k) = f(x_2, x_1, \ldots, x_k)[/latex].
Однако если мы возьмем среднее данного решения, мы получим решение [latex]\frac{x_1+x_2}{2}, \frac{x_1+x_2}{2}, x_3, \ldots, x_k[/latex], не являющееся эквивалентным! Если исходное решение является оптимальным, данное среднее решение, вероятно, будет неоптимальным. Следовательно, целевая функция не может быть выпуклой, потому что для выпуклой функции среднее оптимального решения также является оптимальным решением.
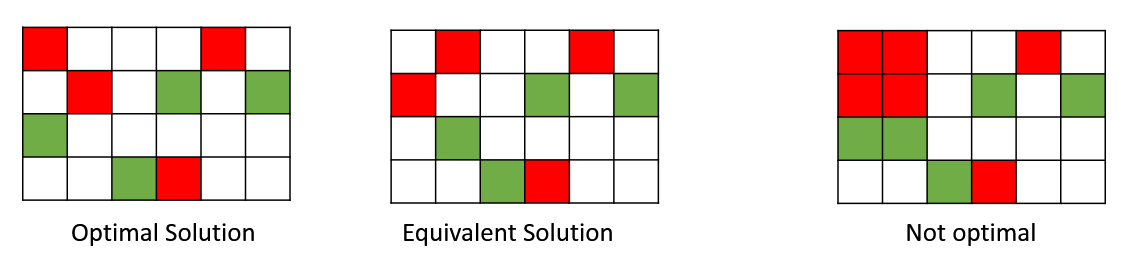
Optimal Solution – оптимальное решение Equivalent Solution – эквивалентное решение Not optimal – неоптимальное решение
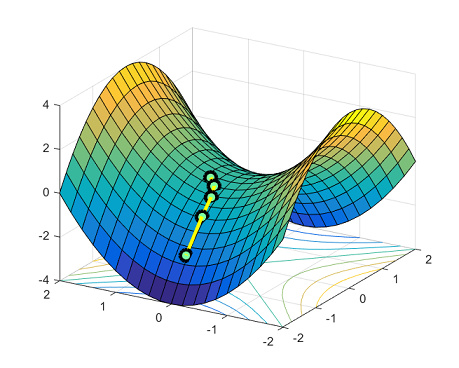
Существует экспоненциально много глобально оптимальных решений, являющихся перестановками одного и того же решения. Седловые точки естественным образом возникают на путях, соединяющих данные изолированные локальные минимумы. На рисунке ниже представлена функция [latex]y = x_1^4-2x_1^2 + x_2^2[/latex]: мы видим два симметричных локальных минимума [latex](-1,0)[/latex] и [latex](1,0)[/latex], между которыми находится седловая точка [latex](0,0)[/latex].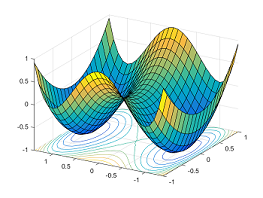
Выбираемся из седловых точек
Чтобы оптимизировать описанные выше невыпуклые функции со множеством седловых точек, алгоритм оптимизации должен прогрессировать даже оказавшись в седловой точке. Простейшим решением является разложение в ряд Тейлора второго порядка:
[latex]f(y) \approx f(x) + \left<\nabla f(x), y-x\right>+\frac{1}{2} (y-x)^\top \nabla^2 f(x) (y-x)[/latex]
Если градиент [latex]\nabla f(x)[/latex] равен [latex]\vec{0}[/latex], мы можем найти вектор [latex]u[/latex], такой, что [latex]u^\top \nabla^2 f(x) u < 0[/latex]. Тогда, если [latex]y = x+\eta u[/latex], значение функции [latex]f(y)[/latex], вероятно, будет меньше. Многие алгоритмы оптимизации, такие как метод доверительных областей (trust region algorithm) и кубическая регуляризация (cubic regularization), используют эту идею и способны выходить из седловых точек за полиномиальное время.
Строго седловые функции
Как мы уже сказали, в общем случае, NP-трудно найти локальный минимум, причем многие алгоритмы могут остановиться в седловой точке. Сколько же нужно шагов, чтобы выбраться из седловой точки? Это зависит от того, насколько корректна (well-behaved) седловая точка. Интуитивно, седловая точка [latex]x[/latex] является корректной, если существует такое направление [latex]u[/latex], для которого слагаемое второго порядка [latex]u^\top \nabla^2 f(x) u[/latex] значительно меньше нуля. Геометрически это означает, что имеет место крутой спуск, в направлении которого значение функция уменьшается. Чтобы количественно оценить описанную характеристику, в нашей публикации [Ge et al.] мы ввели понятие строго седловой функции (strict saddle function) (эта концепция также рассматривается в работе [Sun et al.]).
Функция [latex]f(x)[/latex] является строго седловой, если все точки [latex]x[/latex] удовлетворяют хотя бы одному из следующих условий:
- Градиент [latex]\nabla f(x)[/latex] имеет большое значение.
- Гессиан [latex]\nabla^2 f(x)[/latex] имеет отрицательное собственное значение.
- Точка [latex]x[/latex] находится вблизи локального минимума.
По сути, локальная область каждой точки [latex]x[/latex] соответствует одному из представленных ниже вариантов:
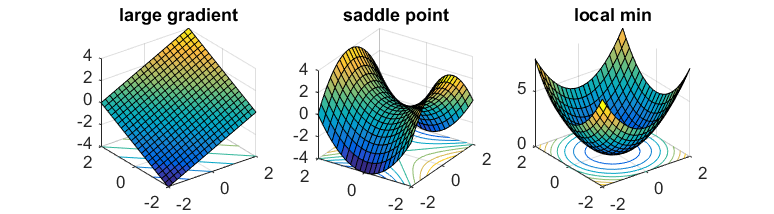
large gradient – большой градиент saddle point – седловая точка local min – локальный минимум
Для таких функций метод доверительных областей и кубическая регуляризация способны эффективно находить локальный минимум.
Теорема (неформальная). Существуют алгоритмы полиномиального времени, позволяющие найти локальный минимум строго седловой функции.
Какие же функции являются строго седловыми? Строго седловые функции имеют место в таких задачах, как: разложение тензоров [Ge et al.], обучение словаря (dictionary learning) и восстановление фазы (phase retrieval) [Sun et al.].
Метод первого порядка, позволяющий преодолевать седловые точки
Метод доверительных областей является очень мощными инструментом. Однако этот метод вычисляет вторую производную целевой функции, что зачастую требует слишком много вычислительных ресурсов. Может ли алгоритм, оперирующий лишь градиентом, преодолеть седловую точку?
Эта задача может показаться сложной, поскольку градиент в седловой точке равен [latex]\vec{0}[/latex] и не дает нам никакой информации. Однако здесь нам поможет тот факт, что положение в седловой точке является очень неустойчивым: если положить воображаемый шарик в седловую точку, а затем слегка подтолкнуть его, – шарик, скорее всего, скатится вниз, покинув седловую точку! Безусловно, необходимо формализовать эту идею для случая большой размерности, поскольку наивный подход для поиска направления, вероятно, потребует вычисления наименьшего собственного вектора (eigenvector) гессиана.
Чтобы формализовать нашу идею, мы используем так называемый шумный градиентный спуск (noisy gradient descent):
[latex]y = x — \eta \nabla f(x) + \epsilon[/latex]
Здесь [latex]\epsilon[/latex] представляет собой вектор шума со средним значением, равным 0. Этот вектор обеспечит первоначальный толчок, в результате которого наш воображаемый шарик начнет скатываться по склону.
На самом деле, зачастую намного легче вычислить шумный градиент, чем истинный градиент. Этот факт лежит в основе алгоритма стохастического градиентного спуска (stochastic gradient descent). Многие работы по данной теме показывают, что шум не оказывает отрицательного воздействия на сходимость в случае выпуклой оптимизации. В случае же невыпуклой оптимизации шум улучшает сходимость, поскольку выталкивает алгоритм из седловых точек. Это не недостаток, это полезное свойство!
Ранее не был известен приемлемый верхний предел количества итераций, необходимых для преодоления седловых точек и достижения локального минимума. В нашей работе [Ge et al.] мы показали следующее:
Теорема (неформальная). Шумный градиентный спуск позволяет достичь локального минимума строго седловой функции за полиномиальное время.
Полиномиальная зависимость от размерности n и наименьшего собственного значения гессиана создают определенные неудобства на практике. Поиск оптимальной скорости сходимости для строго седловых задач остается открытой проблемой.
В недавней работе [Lee et al.] было показано, что даже без добавления шума, градиентный спуск не сойдется ни к одной строго седловой точке, если исходная точка выбрана случайным образом. Однако результаты этой работы опираются на теорему об устойчивом многообразии (stable manifold theorem) из теории динамических систем, которая не оговаривает верхний предел количества шагов.
Вырожденные седловые точки
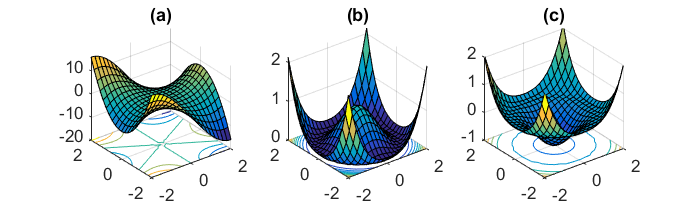
Мы рассмотрели алгоритмы, справляющиеся с простыми седловыми точками. Тем не менее в контексте невыпуклых задач могут иметь место намного более сложные поверхности, где присутствуют вырожденные седловые точки – точки, гессиан которых является положительно полуопределенным и имеет нулевые собственные значения. Подобная вырожденная структура обычно указывает на сложную седловую точку (например, обезьянье седло (monkey saddle), рис. (a)) или множество связанных седловых точек (рис. (b), (c)). В работе [Anandkumar, Ge] мы предложили алгоритм, способный работать с некоторыми вырожденными седловыми точками.
Поверхности невыпуклых функций могут быть очень сложными, соответственно, в этой области по-прежнему остается много открытых вопросов. Какие еще функции являются строго седловыми? Как создавать алгоритмы оптимизации, способные справляться с вырожденными седловыми точками и даже с ложными локальными минимумами? Мы надеемся, что данная тема привлечет внимание многих новых исследователей, которые помогут найти ответы на эти вопросы!
