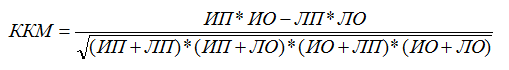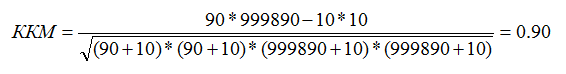Оценка качества классификационных моделей — сложная и трудоемкая задача. Сперва аналитик оценивает робастность классификационной модели с помощью таких средств, как AIC-BIC, площадь под ROC-кривой, критерий согласия Колмогорова-Смирнова и др. Следующим логическим шагом является оценка точности модели. Чтобы понять, почему эта задача является достаточно сложной, давайте рассмотрим базовые концепции.
Выход модели
В большинстве случаев классификационные модели, например, логистическая регрессия (logistic regression), дают на выходе вероятности в интервале от 0 до 1 вместо значений целевой переменой, таких как Да/Нет и т.п. Чтобы оценить точность модели, полученные вероятности необходимо преобразовать в значения целевой переменной. Давайте рассмотрим этот процесс на примере, представленном ниже.
Цель. Создать классификационную модель, идентифицирующую мошеннические операции.
Результат. Разбиение операций на 2 класса: мошеннические и добросовестные.
Оценивание модели. Сравнение результатов классификации с фактическими данными.
Набор данных. Количество операций: 1000000. Количество мошеннических операций: 100. Количество добросовестных операций: 999900.
Мошеннические операции составляют всего 0.01% от всех операций. Таким образом, данная задача является типичным примером задачи с несбалансированными классами. Несбалансированные классы имеют место в задачах классификации, где количество наблюдений, относящихся к одному классу, значительно отличается от количества наблюдений, относящихся к другому классу.
Предположим, мы создали модель, которая классифицировала 95% операций как добросовестные, и все эти операции действительно оказались добросовестными. Звучит неплохо, однако мы не должны слишком радоваться по этому поводу, поскольку мошеннические операции составляют всего 0.01% операций, в то время как наша модель отнесла к классу мошеннических 5% операций.
Сравнив прогнозы модели с фактическими данными, мы получим 4 группы прогнозов:
- Истинноположительные (ИП). Мошеннические операции, классифицированные, как мошеннические.
- Истинноотрицательные (ИО). Добросовестные операции, классифицированные, как добросовестные.
- Ложноположительные (ЛП). Добросовестные операции, классифицированные, как мошеннические.
- Ложноотрицательные (ЛО). Мошеннические операции, классифицированные, как добросовестные.
Популярным способом представления этой информации является таблица сопряженности:
| Количество истинноположительных | Количество ложноотрицательных |
| Количество ложноположительных | Количество истинноотрицательных |
Как мы уже говорили, обычно классификационные модели дают на выходе вероятности. Ниже представлены первые 5 строк набора данных и прогнозы модели:
| Операция | Фактический класс операции | Прогноз |
| 1 | Добросовестная | 0.45 |
| 2 | Добросовестная | 0.10 |
| 3 | Мошенническая | 0.67 |
| 4 | Добросовестная | 0.60 |
| 5 | Добросовестная | 0.11 |
Предположим, что в качестве пороговой вероятности мы выбрали значение 0.5. То есть, если предсказанная моделью вероятность больше или равна 0.5, мы считаем операцию мошеннической, если меньше 0.5 – добросовестной. Соответственно, представленная выше таблица примет следующий вид:
| Операция | Фактический класс операции | Прогноз |
| 1 | Добросовестная | Добросовестная |
| 2 | Добросовестная | Добросовестная |
| 3 | Мошенническая | Мошенническая |
| 4 | Добросовестная | Мошенническая |
| 5 | Добросовестная | Добросовестная |
Обобщим прогнозы модели для полного набора данных с помощью таблицы сопряженности:
| ИП = 90 | ЛО = 10 |
| ЛП = 10 | ИО = 999890 |
Мы видим, что в таблице сопряженности нет ячеек с нулевыми значениями. Так насколько же хорош этот результат? Стремимся ли мы к тому, чтобы ЛП = 0 и ЛО = 0? Это зависит от цели прогноза.
Рассмотрим сценарий, где мы, как маркетинговые аналитики, хотели бы идентифицировать пользователей, которые склонны совершить покупку, но еще не совершили ее. Эти пользователи по своим характеристикам очень близки к пользователям, уже совершившим покупку. Таким образом, модель предскажет, что данные пользователи совершат покупку, хотя на самом деле это не произойдет. То есть, эти прогнозы будут ложноположительными. Следовательно, ненулевое значение ЛП также может быть полезно для нас. Как видите, вывод о качестве модели зависит от цели прогнозирования.
Основные метрики
Поскольку мы уже разобрались, как интерпретировать таблицу сопряженности, теперь давайте рассмотрим распространенные метрики, применяемые для оценивания качества классификационных моделей.
- Чувствительность (полнота)
Чувствительность (sensitivity), также известная, как полнота (recall), вычисляется по следующей формуле:
Чувствительность = ИП / (ИП + ЛО)
Поскольку формула не учитывает ЛП и ИО, чувствительность может дать нам смещенную оценку, особенно в случае несбалансированных классов. В задаче выявления мошенничества чувствительность представляет собой процент правильно классифицированных мошеннических операций от общего фактического количества мошеннических операций.
Чувствительность = 90 / (90 + 10) = 0.90
- Специфичность
Специфичность (specificity) вычисляется по следующей формуле:
Специфичность = ИО / (ИО + ЛП)
Поскольку формула не учитывает ЛО и ИП, специфичность может дать нам смещенную оценку, особенно в случае несбалансированных классов. В задаче выявления мошенничества специфичность представляет собой процент правильно классифицированных добросовестных операций от общего фактического количества добросовестных операций.
Специфичность = 999890 / (999890 + 10) = 1
- Точность
Точность (precision) вычисляется по следующей формуле:
Точность = ИП / (ИП + ЛП)
Поскольку формула не учитывает ЛО и ИО, точность, как и предыдущие метрики, может дать нам смещенную оценку, особенно в случае несбалансированных классов. В задаче выявления мошенничества точность представляет собой процент правильно классифицированных мошеннических операций от общего количества операций, классифицированных, как мошеннические.
Точность = 90 / (90 + 10) = 0.90
- F-мера
F-мера (F1 score) представляет собой совместную оценку точности и полноты. Данная метрика вычисляется по следующей формуле:
F-мера = 2 * Точность * Полнота / (Точность + Полнота)
F-мера позволяет получить более сбалансированную характеристику модели, чем три метрики, рассмотренные выше. Однако, поскольку F-мера не учитывает ИО, эта метрика также может дать смещенную оценку в случае сценария, рассмотренного ниже.
F-мера = 2 * 0.90 * 0.90 / (0.90 + 0.90) = 0.90
- Коэффициент корреляции Мэтьюса
В отличие от остальных метрик, рассмотренных выше, коэффициент корреляции Мэтьюса (ККМ, Matthews сorrelation сoefficient) учитывает значения из всех ячеек матрицы сопряженности и вычисляется по следующей формуле:
ККМ может принимать значения из интервала от -1 до +1. Модель, получившая оценку +1, является идеальной. Модель, получившая оценку -1, является очень слабой. Одним из ключевых свойств ККМ является легкость интерпретации.
Сравнение метрик
Далее мы оценим классификационную модель с помощью описанных выше метрик при различных пороговых вероятностях и сравним результаты.
Сценарий A. Пороговая вероятность 0.5.
Таблица сопряженности:
| ИП = 90 | ЛО = 10 |
| ЛП = 10 | ИО = 999890 |
Оценки модели, полученные с помощью различных метрик:
| Чувствительность | Специфичность | Точность | F-мера | ККМ |
| 0.90 | 1.00 | 0.90 | 0.90 | 0.90 |
Сценарий B. Пороговая вероятность 0.4.
Таблица сопряженности:
| ИП = 90 | ЛО = 10 |
| ЛП = 1910 | ИО = 997990 |
Мы видим, что при сценарии B существенно возросло значение ЛП по сравнению со сценарием A. Следовательно, мы должны наблюдать ухудшение оценок.
Оценки модели, полученные с помощью различных метрик:
| Чувствительность | Специфичность | Точность | F-мера | ККМ |
| 0.90 | 1.00 | 0.05 | 0.09 | 0.20 |
Следует отметить, что значения чувствительности и специфичности не изменились.
Сценарий C. Пороговая вероятность 0.6.
Таблица сопряженности:
| ИП = 90 | ЛО = 1910 |
| ЛП = 10 | ИО = 997990 |
Мы видим, что при сценарии C существенно возросло значение ЛО по сравнению со сценарием A. Следовательно, мы должны наблюдать ухудшение оценок.
Оценки модели, полученные с помощью различных метрик:
| Чувствительность | Специфичность | Точность | F-мера | ККМ |
| 0.05 | 1.00 | 0.90 | 0.09 | 0.20 |
Отметим, что значения специфичности и точности не изменились.
Основываясь на нашем сравнительном анализе, можно сделать вывод о том, что предпочтительными метриками являются F-мера и ККМ. Однако необходимо рассмотреть еще один сценарий.
В рассмотренных выше сценариях наша модель предсказывала вероятность того, что данная операция является мошеннической. Если модель будет предсказывать вероятность того, что данная операция является добросовестной, мы получим сценарий D.
Сценарий D. Пороговая вероятность 0.5.
Таблица сопряженности:
| ИП = 999890 | ЛО = 10 |
| ЛП = 10 | ИО = 90 |
Данная таблица аналогична таблице из сценария A, за исключением того, что значения для положительных и отрицательных прогнозов поменялись местами. В идеале оценки должны быть одинаковы для сценариев A и D.
Оценки модели, полученные с помощью различных метрик:
| Чувствительность | Специфичность | Точность | F-мера | ККМ |
| 1 | 0.90 | 1 | 1 | 0.90 |
Как видим, все оценки, кроме ККМ, изменились по сравнению со сценарием A.
Итоговая таблица для всех сценариев:
| Сценарий | Чувствительность | Специфичность | Точность | F-мера | ККМ |
| A | 0.90 | 1.00 | 0.90 | 0.90 | 0.90 |
| B | 0.90 | 1.00 | 0.05 | 0.09 | 0.20 |
| C | 0.05 | 1.00 | 0.90 | 0.09 | 0.20 |
| D | 1 | 0.90 | 1 | 1 | 0.90 |
Заключение
Если вы, как аналитик, ищите метрику, чтобы оценить и максимизировать общее качество классификационной модели, оптимальным вариантом будет коэффициент корреляции Мэтьюса. Данная метрика не только легко интерпретируется, но также является устойчивой по отношению к смене класса, вероятность которого предсказывает модель.
Перевод Станислава Петренко