Сущность машинного обучения – это распознавание закономерностей в данных. Для этого требуются три компонента: данные, программное обеспечение и математика. Вы спросите, что можно сделать с помощью 7 строк кода? Отвечу вам: очень многое.
Уложиться в 7 строк кода при решении задачи глубокого обучения нам позволит применение библиотек, реализующих слои абстракции. Подобные библиотеки называются «фреймворками». Сегодня нашими инструментами будут TensorFlow и TFLearn.
Абстракция – это неотъемлемое свойство программного обеспечения. Например, приложение, в котором вы сейчас читаете эту статью, является слоем абстракции над вашей операционной системой, умеющей читать файлы, передавать данные и др. Далее следуют функции более низкого уровня. Наконец, существует код уровня процессора, который оперирует битами, – здесь работает «голое железо».
Фреймворк – это слой абстракции
Краткость нашего кода будет обеспечена с помощью фреймворка TFLearn, являющегося надстройкой над TensorFlow, в свою очередь являющегося надстройкой над Python. Как обычно, чтобы упростить организацию кода, мы будем работать в блокноте IPython.
Начнем с самого начала
В статье «Как работают нейронные сети» («How Neural Networks Work») была создана нейронная сеть на Python без использования фреймворков, и продемонстрирован процесс обучения, в рамках которого нейронная сеть обучается находить закономерности в данных. Мы намеренно использовали очень простые «игрушечные данные», закономерности в которых видны невооруженным глазом.
Блокнот, содержащий код этого проекта, реализующего «нулевой уровень абстракции», находится здесь. Каждая математическая операция в модели подробно описана.
Усовершенствовав эту модель путем реализации 2 скрытых слоев и градиентного спуска (gradient descent) (аналогично проекту для анализа текста), мы получаем около 80 строк кода, опять же без применения фреймворков. Эта нейронная сеть является глубокой, поскольку содержит скрытые слои.
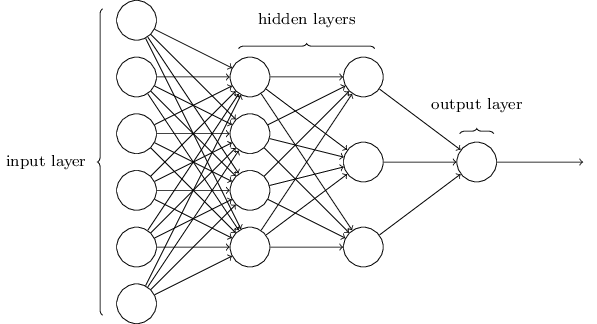
Нейронная сеть с двумя скрытыми слоями
Логика нашей модели достаточно проста, но ее реализация является трудоемкой. Большая часть кода относится к процессу обучения:
# convert output of sigmoid function to its derivative
def sigmoid_output_to_derivative(output):
return output*(1-output)
def think(sentence, show_details=False):
x = bow(sentence.lower(), words, show_details)
if show_details:
print ("sentence:", sentence, "\n bow:", x)
# input layer is our bag of words
l0 = x
# matrix multiplication of input and hidden layer
l1 = sigmoid(np.dot(l0, synapse_0))
# output layer
l2 = sigmoid(np.dot(l1, synapse_1))
return l2
def train(X, y, hidden_neurons=10, alpha=1, epochs=50000, dropout=False, dropout_percent=0.5):
print ("Training with %s neurons, alpha:%s, dropout:%s %s" % (hidden_neurons, str(alpha), dropout, dropout_percent if dropout else '') )
print ("Input matrix: %sx%s Output matrix: %sx%s" % (len(X),len(X[0]),1, len(classes)) )
np.random.seed(1)
last_mean_error = 1
# randomly initialize our weights with mean 0
synapse_0 = 2*np.random.random((len(X[0]), hidden_neurons)) - 1
synapse_1 = 2*np.random.random((hidden_neurons, len(classes))) - 1
prev_synapse_0_weight_update = np.zeros_like(synapse_0)
prev_synapse_1_weight_update = np.zeros_like(synapse_1)
synapse_0_direction_count = np.zeros_like(synapse_0)
synapse_1_direction_count = np.zeros_like(synapse_1)
for j in iter(range(epochs+1)):
# Feed forward through layers 0, 1, and 2
layer_0 = X
layer_1 = sigmoid(np.dot(layer_0, synapse_0))
if(dropout):
layer_1 *= np.random.binomial([np.ones((len(X),hidden_neurons))],1-dropout_percent)[0] * (1.0/(1-dropout_percent))
layer_2 = sigmoid(np.dot(layer_1, synapse_1))
# how much did we miss the target value?
layer_2_error = y - layer_2
if (j% 10000) == 0 and j > 5000:
# if this 10k iteration's error is greater than the last iteration, break out
if np.mean(np.abs(layer_2_error)) < last_mean_error:
print ("delta after "+str(j)+" iterations:" + str(np.mean(np.abs(layer_2_error))) )
last_mean_error = np.mean(np.abs(layer_2_error))
else:
print ("break:", np.mean(np.abs(layer_2_error)), ">", last_mean_error )
break
# in what direction is the target value?
# were we really sure? if so, don't change too much.
layer_2_delta = layer_2_error * sigmoid_output_to_derivative(layer_2)
# how much did each l1 value contribute to the l2 error (according to the weights)?
layer_1_error = layer_2_delta.dot(synapse_1.T)
# in what direction is the target l1?
# were we really sure? if so, don't change too much.
layer_1_delta = layer_1_error * sigmoid_output_to_derivative(layer_1)
synapse_1_weight_update = (layer_1.T.dot(layer_2_delta))
synapse_0_weight_update = (layer_0.T.dot(layer_1_delta))
if(j > 0):
synapse_0_direction_count += np.abs(((synapse_0_weight_update > 0)+0) - ((prev_synapse_0_weight_update > 0) + 0))
synapse_1_direction_count += np.abs(((synapse_1_weight_update > 0)+0) - ((prev_synapse_1_weight_update > 0) + 0))
synapse_1 += alpha * synapse_1_weight_update
synapse_0 += alpha * synapse_0_weight_update
prev_synapse_0_weight_update = synapse_0_weight_update
prev_synapse_1_weight_update = synapse_1_weight_update
now = datetime.datetime.now()
# persist synapses
synapse = {'synapse0': synapse_0.tolist(), 'synapse1': synapse_1.tolist(),
'datetime': now.strftime("%Y-%m-%d %H:%M"),
'words': words,
'classes': classes
}
synapse_file = "synapses.json"
with open(synapse_file, 'w') as outfile:
json.dump(synapse, outfile, indent=4, sort_keys=True)
print ("saved synapses to:", synapse_file)
Этот код отлично работал. Затем мы абстрагировали его с помощью фреймворка.
Абстрагируем модель с помощью TensorFlow

В статье «Разоблачение TensorFlow» («TensorFlow demystified») описанная выше сеть была реализована с применением TensorFlow. Еще раз была продемонстрирована способность модели выявлять закономерности в данных.
Абстрагирование позволило существенно упростить код. Например, реализация градиентного спуска и функции потерь сократилась до 2 строк.
# formula for cost (error) cost = tf.reduce_mean( tf.nn.softmax_cross_entropy_with_logits(prediction,y) ) # optimize for cost using GradientDescent optimizer = tf.train.GradientDescentOptimizer(1).minimize(cost)
Весь код можно найти здесь.
Определение модели также упростилось. Математические операции и распространенные функции (например, сигмоида) инкапсулированы во фреймворке.
# our predictive model's definition def neural_network_model(data): # hidden layer 1: (data * W) + b l1 = tf.add(tf.matmul(data,hidden_1_layer['weight']), hidden_1_layer['bias']) l1 = tf.sigmoid(l1) # hidden layer 2: (hidden_layer_1 * W) + b l2 = tf.add(tf.matmul(l1,hidden_2_layer['weight']), hidden_2_layer['bias']) l2 = tf.sigmoid(l2) # output: (hidden_layer_2 * W) + b output = tf.matmul(l2,output_layer['weight']) + output_layer['bias'] return output
Впрочем, если представить себе сложную нейронную сеть, такую как AlexNet, ее реализация даже с применением TensorFlow будет громоздкой.
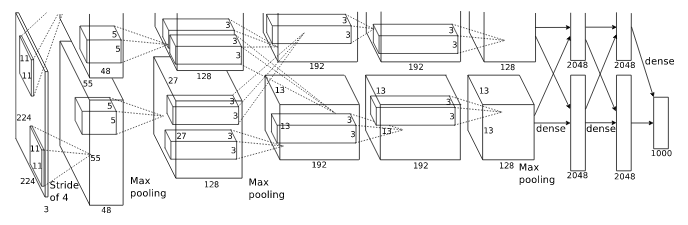
AlexNet
Еще один слой абстракции
Поскольку код по-прежнему является достаточно многословным, мы задействуем еще один слой абстракции, представленный в библиотеке TFLearn. Этот инструмент описывается следующим образом:
TFLearn: библиотека глубокого обучения, реализующая высокоуровневый API для TensorFlow.
Термин «высокоуровневый API» говорит о том, что данная библиотека дает нам более высокий уровень абстракции, что нам и нужно. Теперь наша многослойная нейронная сеть может быть реализована с помощью 7 строк кода.
# Build neural network net = tflearn.input_data(shape=[None, 5]) net = tflearn.fully_connected(net, 32) net = tflearn.fully_connected(net, 32) net = tflearn.fully_connected(net, 2, activation='softmax') net = tflearn.regression(net)
# Define model and setup tensorboard model = tflearn.DNN(net, tensorboard_dir='tflearn_logs') # Start training (apply gradient descent algorithm) model.fit(train_x, train_y, n_epoch=500, batch_size=16, show_metric=True)
Просто великолепно: 5 строк, чтобы задать архитектуру сети (входной слой + 2 скрытых слоя + выходной слой + регрессия), и 2 строки, чтобы обучить ее.
Полный код находится здесь.
Давайте рассмотрим эту реализацию подробно. Вы увидите, что данные и логика идентичны рассмотренной выше реализации, где применялся лишь TensorFlow.
Устанавливаем TFLearn
Убедитесь, что у вас установлен TensorFlow версии не менее 1.0.x, поскольку TFLearn не будет работать с более ранней версией. Выведем версию:
import tensorflow as tf tf.__version__
В результате мы должны получить примерно следующее: ‘1.0.1’
Чтобы установить (обновить) TensorFlow и TFLearn выполним следующую команду:
python -m pip install --upgrade tensorflow tflearn
Данные
Далее мы создаем наши «игрушечные» данные, те же самые, что были использованы в рассмотренной выше реализации, где применялся лишь TensorFlow. Обратите внимание, больше нет необходимости формировать валидационный набор данных для использования в процессе обучения, поскольку TFLearn может сделать это за нас.
import numpy as np
import tflearn
import random
def create_feature_sets_and_labels():
# known patterns (5 features) output of [1] of positions [0,4]==1
features = []
features.append([[0, 0, 0, 0, 0], [0,1]])
features.append([[0, 0, 0, 0, 1], [0,1]]) features.append([[0, 0, 0, 1, 1], [0,1]]) features.append([[0, 0, 1, 1, 1], [0,1]]) features.append([[0, 1, 1, 1, 1], [0,1]]) features.append([[1, 1, 1, 1, 0], [0,1]]) features.append([[1, 1, 1, 0, 0], [0,1]]) features.append([[1, 1, 0, 0, 0], [0,1]]) features.append([[1, 0, 0, 0, 0], [0,1]])
features.append([[1, 0, 0, 1, 0], [0,1]]) features.append([[1, 0, 1, 1, 0], [0,1]]) features.append([[1, 1, 0, 1, 0], [0,1]]) features.append([[0, 1, 0, 1, 1], [0,1]]) features.append([[0, 0, 1, 0, 1], [0,1]]) features.append([[1, 0, 1, 1, 1], [1,0]]) features.append([[1, 1, 0, 1, 1], [1,0]]) features.append([[1, 0, 1, 0, 1], [1,0]]) features.append([[1, 0, 0, 0, 1], [1,0]])
features.append([[1, 1, 0, 0, 1], [1,0]]) features.append([[1, 1, 1, 0, 1], [1,0]]) features.append([[1, 1, 1, 1, 1], [1,0]]) features.append([[1, 0, 0, 1, 1], [1,0]]) # shuffle our features and turn into np.array random.shuffle(features) features = np.array(features) # create train and test lists
train_x = list(features[:,0]) train_y = list(features[:,1]) return train_x, train_y
Великолепная семерка
И, наконец, код, реализующий непосредственно глубокое обучение:
# Build neural network net = tflearn.input_data(shape=[None, 5]) net = tflearn.fully_connected(net, 32) net = tflearn.fully_connected(net, 32) net = tflearn.fully_connected(net, 2, activation='softmax') net = tflearn.regression(net)
# Define model and setup tensorboard model = tflearn.DNN(net, tensorboard_dir='tflearn_logs') # Start training (apply gradient descent algorithm) model.fit(train_x, train_y, n_epoch=500, batch_size=16, show_metric=True)
Первые 5 строк задают архитектуру нашей нейронной сети с помощью следующих функций: tflearn.input_data, tflearn.fully_connected, tflearn.regression. Входные данные имеют 5 признаков, мы используем 32 нейрона в каждом скрытом слое, а на выходе получаем вероятности 2 классов.
Далее мы создаем глубокую нейронную сеть на основе заданной архитектуры с помощью tflearn.DNN. Мы используем параметр tensorboard_dir, чтобы задать путь для сохранения журнала.
И, наконец, мы обучаем нашу нейронную сеть. Следует отметить удобный интерфейс отображения метрик в процессе обучения. Далее мы можем изменить значение параметра n_epoch, чтобы оценить его влияние на точность (accuracy).
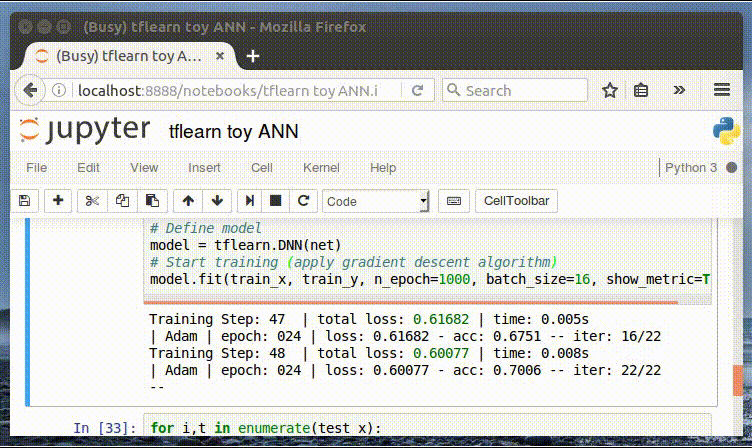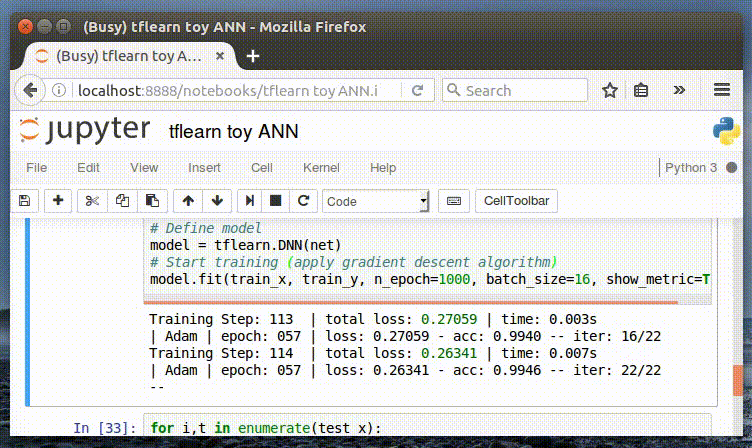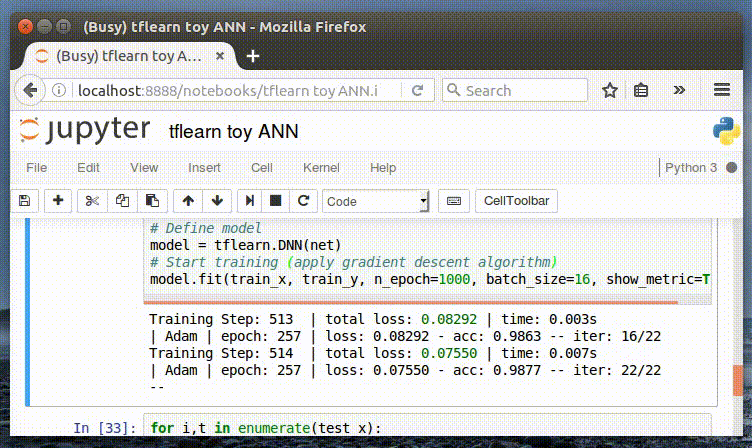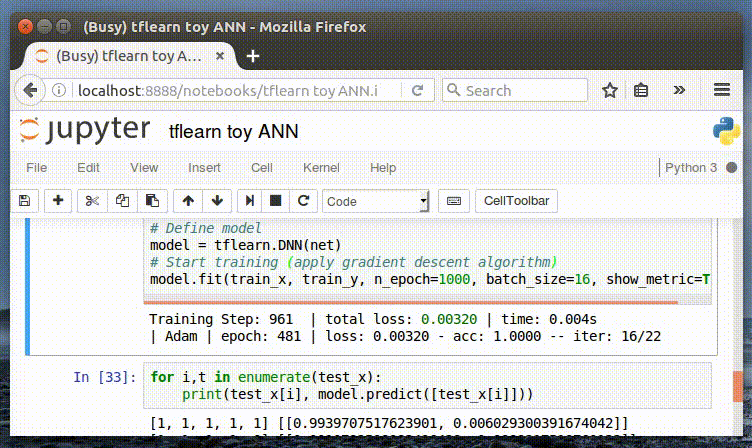
Интерактивное отображение метрик в процессе обучения
Training Step: 1999 | total loss: 0.01591 | time: 0.003s
| Adam | epoch: 1000 | loss: 0.01591 — acc: 0.9997 — iter: 16/22
Training Step: 2000 | total loss: 0.01561 | time: 0.006s
| Adam | epoch: 1000 | loss: 0.01561 — acc: 0.9997 — iter: 22/22
—
Тестируем модель
Теперь мы можем использовать нашу нейронную сеть для прогнозирования. Перед началом обучения обязательно необходимо убедиться в том, что в наборе обучающих данных нет примеров, на которых мы хотим протестировать модель, иначе модель будет «жульничать». Строки, содержащие примеры для тестирования, можно просто закомментировать.
Прогнозируем:
print(model.predict([[0, 0, 0, 1, 1]])) print(model.predict([[1, 0, 1, 0, 1]]))
Результат:
[[0.004509848542511463, 0.9954901337623596]] [[0.9810173511505127, 0.018982617184519768]]
Наша модель правильно распознает закономерность [1, _, _, _, 1], давая на выходе [1, 0].
Для удобства при многократной работе с блокнотом мы сбрасываем граф модели, добавив следующие 2 строки непосредственно перед кодом модели:
# reset underlying graph data import tensorflow as tf tf.reset_default_graph() # Build neural network ...
Благодаря абстрагированию с помощью фреймворка, мы больше не должны тратить время на кропотливую реализацию и можем сосредоточиться на подготовке данных и прогнозировании.
TensorBoard
TFLearn автоматически передает данные в TensorBoard – инструмент визуализации TensorFlow. В tflearn.DNN мы задали путь для журнала, теперь мы можем на него взглянуть:
$ tensorboard --logdir=tflearn_logs Starting TensorBoard b’41' on port 6006 (You can navigate to http://127.0.1.1:6006)
На рисунке ниже представлен граф нашей модели:
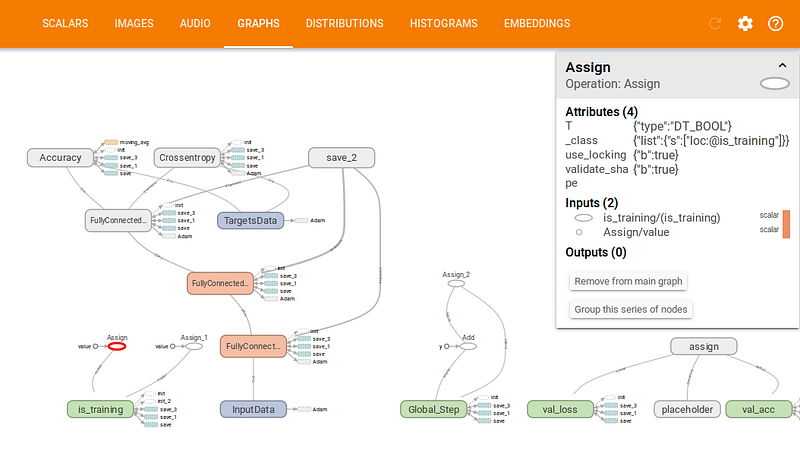
TensorBoard Graphs
Также мы можем увидеть графики функции потерь и точности:
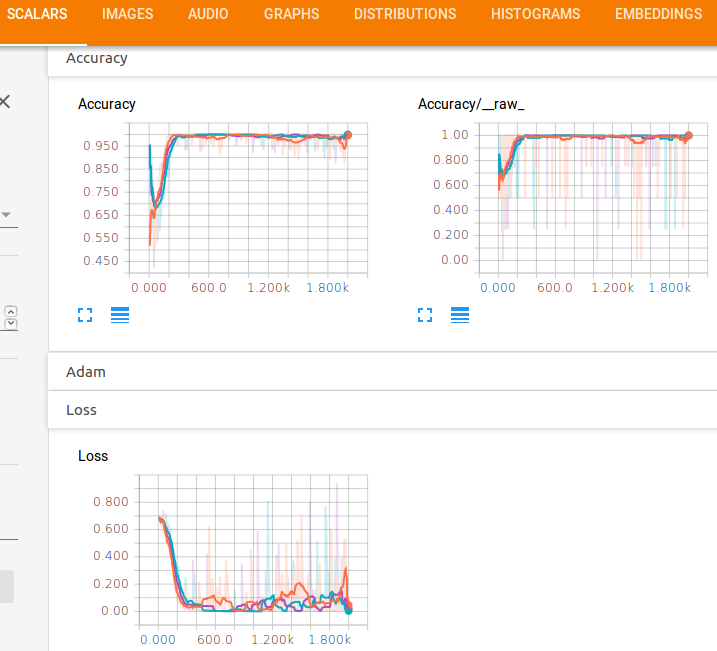
TensorBoard Scalars
Очевидно, что нам не требуется такое большое количество эпох для достижения хорошей точности.
Другие примеры
Теперь давайте посмотрим, как с помощью TFLearn можно реализовать рекуррентную LSTM-сеть (LSTM recurrent neural network). Такие сети обычно используются в тех случаях, когда необходимо обучить модель на последовательности данных с реализацией памяти. В данном случае мы имеем другую архитектуру с применением функции tflearn.lstm, но при этом базовая концепция остается все той же.
# Network building net = tflearn.input_data([None, 100]) net = tflearn.embedding(net, input_dim=10000, output_dim=128) net = tflearn.lstm(net, 128, dropout=0.8) net = tflearn.fully_connected(net, 2, activation='softmax') net = tflearn.regression(net, optimizer='adam', learning_rate=0.001, loss='categorical_crossentropy')
# Training model = tflearn.DNN(net) model.fit(trainX, trainY, validation_set=(testX, testY), show_metric=True, batch_size=32)
Полный код примера доступен здесь.
В качестве еще одного примера давайте рассмотрим реализацию сверточной нейронной сети (convolutional neural network) с помощью TFLearn. Данный тип сетей применяется для распознавания изображений. Как и в других примерах, мы просто задаем последовательность математических операций, определяющих архитектуру сети, а затем обучаем ее.
# Building convolutional network network = input_data(shape=[None, 28, 28, 1], name='input') network = conv_2d(network, 32, 3, activation='relu', regularizer="L2") network = max_pool_2d(network, 2) network = local_response_normalization(network) network = conv_2d(network, 64, 3, activation='relu', regularizer="L2") network = max_pool_2d(network, 2) network = local_response_normalization(network) network = fully_connected(network, 128, activation='tanh') network = dropout(network, 0.8) network = fully_connected(network, 256, activation='tanh') network = dropout(network, 0.8) network = fully_connected(network, 10, activation='softmax') network = regression(network, optimizer='adam', learning_rate=0.01, loss='categorical_crossentropy', name='target')
# Training
model = tflearn.DNN(network)
model.fit({'input': X}, {'target': Y}, n_epoch=20,
validation_set=({'input': testX}, {'target': testY}),
snapshot_step=100, show_metric=True, run_id='convnet_mnist')
Полный код примера доступен здесь.
Начиная изучение нейронных сетей, полезно разобраться в коде, написанном без использования фреймворков. Этот подход позволяет приобрести хорошее понимание внутренних процессов без «черных ящиков». Затем мы можем приступать к применению фреймворков, которые позволяют существенно сократить объем кода.
Фреймворки глубокого обучения упрощают нашу работу, инкапсулируя функции более низкого уровня. По мере развития фреймворков, мы автоматически наследуем все усовершенствования, получая в свое распоряжение мощные функции высокого уровня.
