Автор оригинальной публикации: Эрик Бернхардсон (Erik Bernhardsson)
Перевод Станислава Петренко
Как оказалось, компания MTA, под управлением которой находится Нью-Йоркский метрополитен, предоставляет открытый доступ к прикладному интерфейсу реального времени (real-time API) для сбора информации о движении поездов. Метро всегда привлекало мое внимание, поэтому я просто должен был проанализировать немного данных. Поскольку документация оставляет желать лучшего, ниже представлен образец кода для работы с API:
from google.transit import gtfs_realtime_pb2
import urllib
for feed_id in [1, 2, 11]:
feed = gtfs_realtime_pb2.FeedMessage()
response = urllib.urlopen('http://datamine.mta.info/mta_esi.php?key=%s&feed_id=%d' % (os.environ['MTA_KEY'], feed_id))
feed.ParseFromString(response.read())
print feed
Я запустил отслеживание всех поездов метро и совершенно забыл об этом. Несколько недель спустя было собрано 3 ГБ данных обо всех прибытиях поездов следующих маршрутов: 1, 2, 3, 4, 5, 6, L, SI и GC (SI – железная дорога Статен-Айленда, GC – челнок 42-й улицы).
Поиграем с данными!
Для начала посмотрим на движение поездов по маршруту 1 в течение определенного интервала времени:

Я начал анализировать эти данные, чтобы понять, в какой момент времени ожидание поезда метро превращается из «инвестиций» в «невозвратные затраты». В частности, меня интересовала оптимальная стратегия ожидания. Интуиция подсказывала, что существует некоторый момент времени T, такой, что при приближении к нему дополнительное время ожидания уменьшается, а после него – возрастает. До наступления момента T, каждая секунда ожидания приближает нас к следующему поезду. Если же поезда все еще нет после наступления момента T, вероятно, возникли какие-то проблемы, следовательно, ждать больше нет смысла.
Это предположение подтвердилось. Но для начала давайте посмотрим на распределение временных интервалов между прибытиями двух поездов P(t):
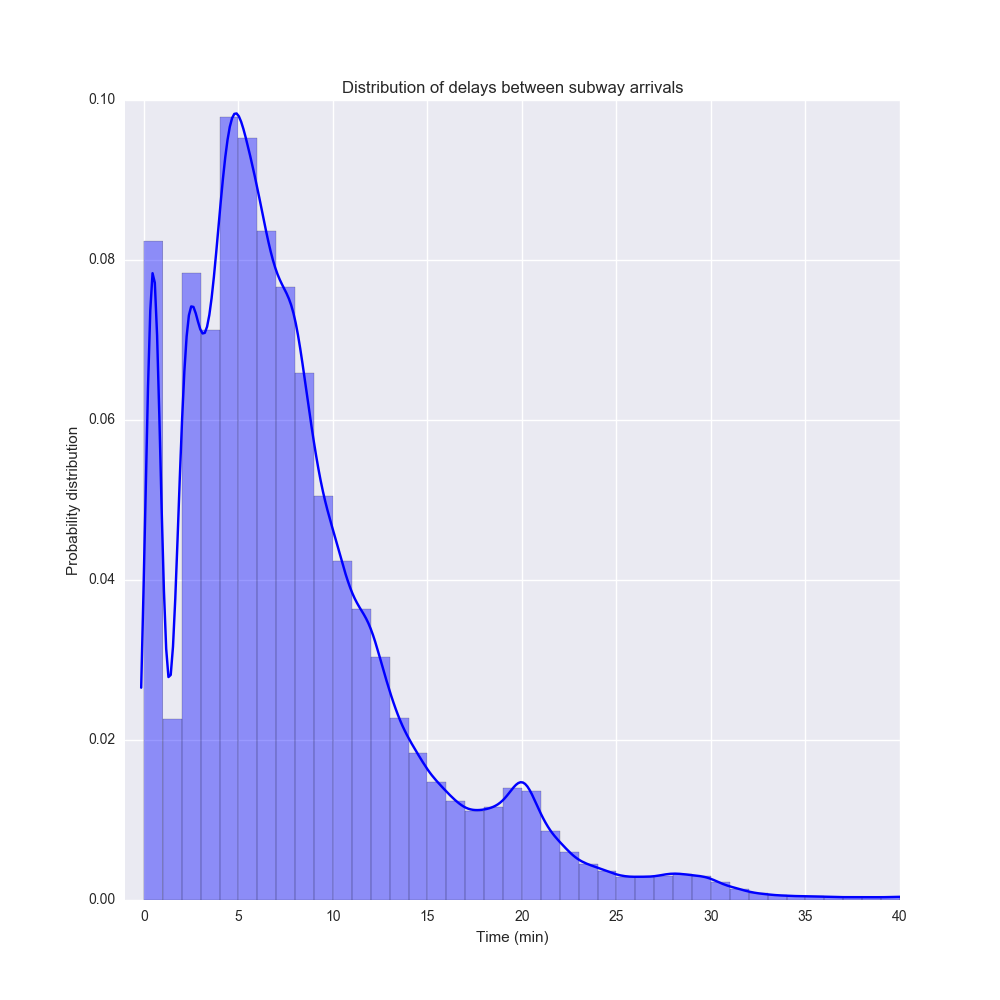
Визуализация выполнена с помощью функции distplot из пакета Seaborn и представляет собой гистограмму (с бинами в 1 минуту) в комбинации с ядерной оценкой плотности распределения (kernel density estimation).
Интересный факт заключается в том, что распределение имеет мультимодальный характер. Следует отметить два пика в районах 5 и 20 минут, которые, вероятно, характеризуют трафик в час пик и в ночное время соответственно. Кроме того, имеет место пик сразу после нуля, что, вероятно, соответствует ситуации, когда в час пик поезда прибывают почти друг за другом.
Обратите внимание, выше речь идет не о времени ожидания, а о временном интервале между прибытиями двух поездов. Время ожидания мы рассмотрим далее. Если предположить, что пассажир с равной вероятностью случайным образом выбирает станцию метро и время суток, тогда время ожидания поезда имеет представленное ниже распределение:
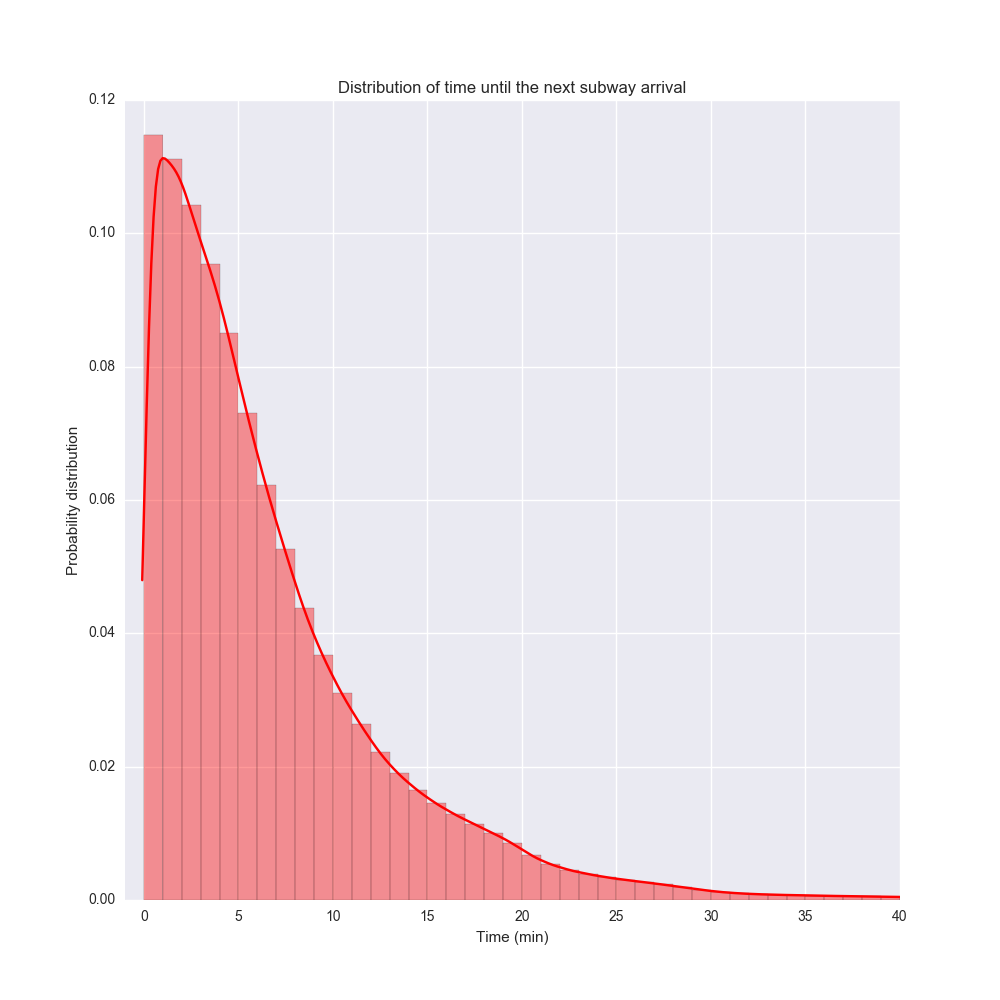
Наиболее вероятное время ожидания (мода) составляет 1 минуту, хотя медиана и среднее имеют намного большие значения.
Взаимосвязь между двумя кривыми
В общем случае распределение временных интервалов между событиями P(t) можно преобразовать в распределение времени ожидания следующего события Q(t) с помощью соотношения:
[latex]Q(t) = \frac{ \int_t^\infty P(s) ds }{ \int_0^\infty sP(s) ds }[/latex]
Этот подход может быть немного неточным, поэтому не используйте его в ответственных случаях. Хотя, похоже, он работает. Если применить дельта-функцию Дирака (Dirac delta function) [latex]P(t) = \delta(t-d)[/latex], мы получим: [latex]Q(t) = 1/d, 0 \le t \le d[/latex]. На практике я реализовал это просто с помощью семплирования.
Время ожидания в зависимости от маршрута
Давайте визуализируем распределения времени ожидания для каждого маршрута с помощью скрипичных диаграмм (violin plot), воспользовавшись функцией violinplot из пакета Seaborn.
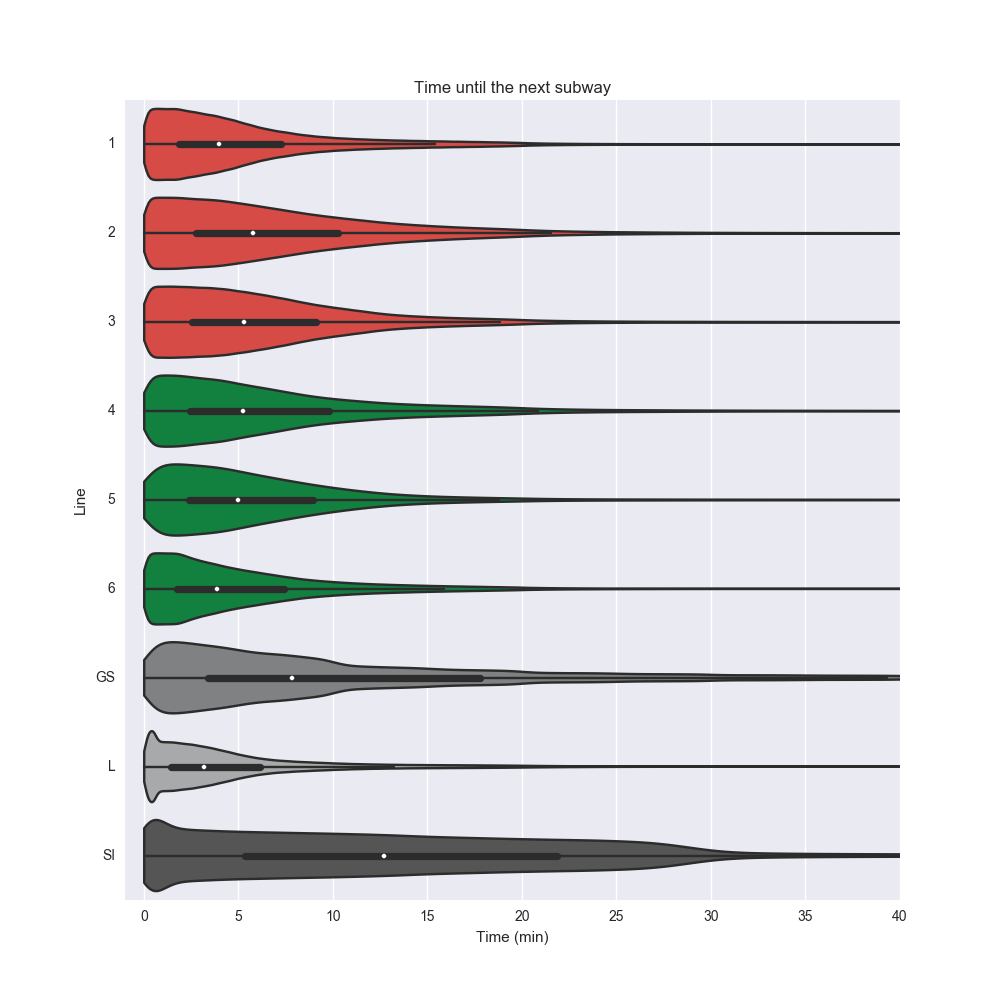
Следует отметить, что маршрут L показывает лучшие результаты, несмотря на распространенное мнение о серьезных задержках на данном маршруте. В частности, мы видим, что для L медиана времени ожидания наименьшая из всех, причем даже крайние значения выгодно отличаются от соответствующих значений для других маршрутов.
(К слову, на диаграмме использована официальная цветовая схема MTA. А вы знали, что цвет маршрута L не строго серый, а на самом деле #A7A9AC, то есть немного более синий? Удивительно.)
Время ожидания в зависимости от времени суток
Очевидно, что время суток является очень важным фактором, поэтому давайте посмотрим на время ожидания в различное время суток. Каждому моменту времени в сутках соответствует некоторое распределение времени ожидания, поэтому мы визуализируем различные квантили и посмотрим на их изменение в течение суток.
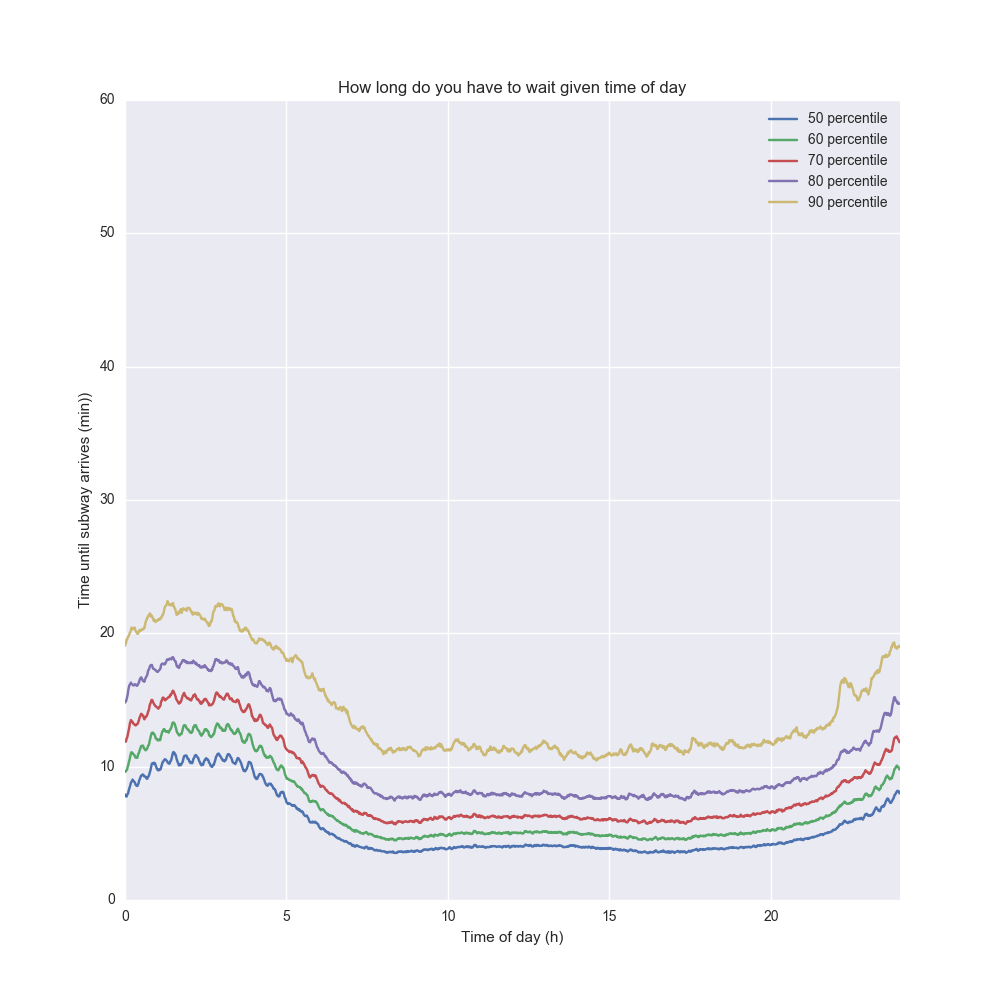
Синяя кривая представляет 50-ю процентиль, то есть медиану времени ожидания. Желтая кривая представляет 90-ю процентиль, что означает, что в 90% случаев время ожидания не превысит данное значение. На практике выбор кривой для оценки времени ожидания зависит от нашего отношения к риску (risk aversion): если мы должны успеть на самолет, тогда следует ориентироваться на 90-ю процентиль, если же опоздание не будет иметь существенных последствий, – можно ориентироваться на 50-ю процентиль.
Следует отметить, что время ожидания максимально в предрассветные часы, что неудивительно, и минимально в интервале от 7 утра до 7 вечера.
Ожидание поезда метро и «невозвратные затраты»
Предположим, мы ждем поезд уже 10 минут, и он еще не пришел. Следует ли в этот момент отказаться от поездки на метро? Вероятно, нет. Однако если прошел уже целый час, скорее всего, ждать дальше нет смысла. До определенного момента ожидание поезда – это «инвестирование» в более раннее прибытие в место назначения.
Здесь также играет роль наше отношение к риску: если мы должны успеть на самолет, тогда в какой-то момент можно просто сдаться и взять такси. Таким образом, если допустить, что мы ждем поезд уже в течение t минут, сколько еще времени нам придется ждать?
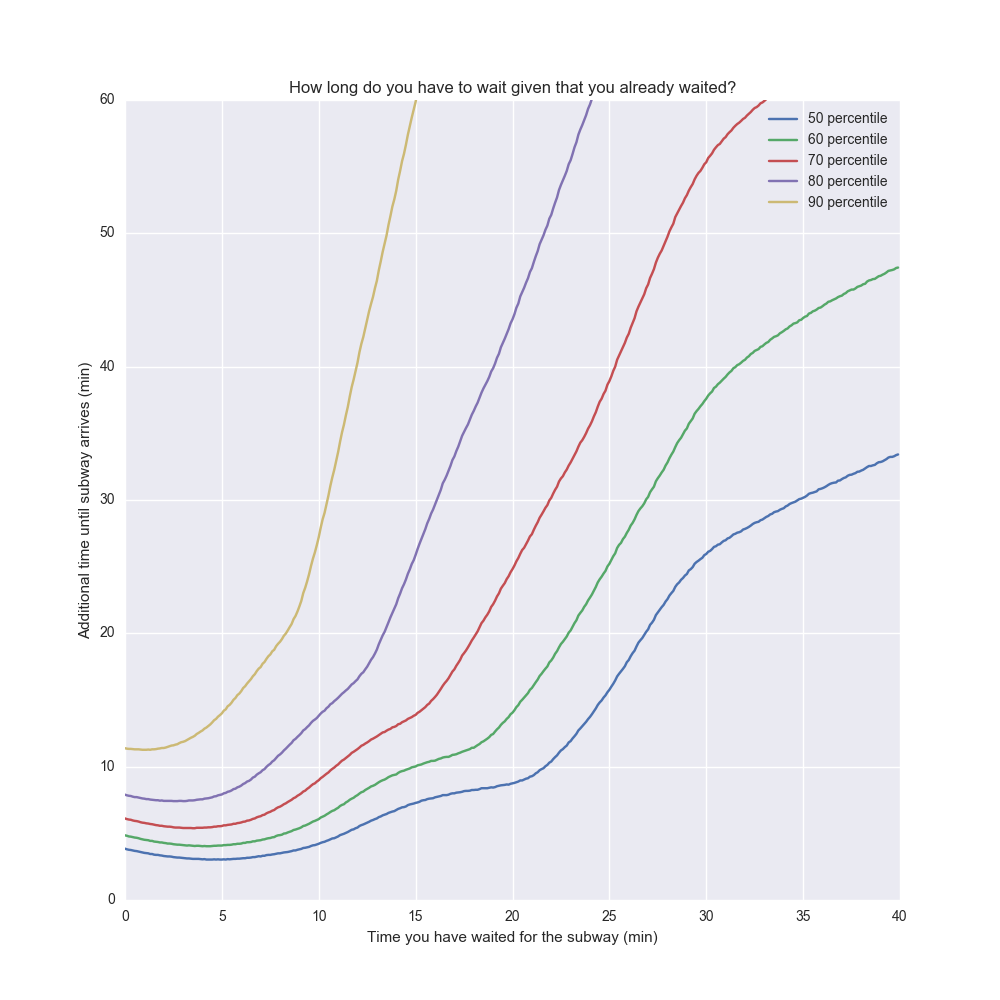
Здесь имеет место определенное смещение, поскольку большее время ожидания наблюдается в ночные часы. Это явление представляет собой искажающий фактор (confounding factor), поэтому я ограничил данные для представленной выше диаграммы интервалом от 7 утра до 7 вечера.
Интересный вывод заключается в следующем: после пяти минут ожидания, чем дольше мы ждем, тем дольше придется еще ждать. Если мы прождали поезд 15 минут, медиана дополнительного времени ожидания составляет 8 минут. Однако если спустя 8 минут поезд все еще не пришел, медиана дополнительного времени ожидания составит уже 12 минут.
Так когда же следует сдаться? Ответ зависит от того, сколько времени мы готовы посвятить ожиданию. Время, уже потраченное на ожидание, представляет собой «невозвратные затраты», и поэтому не имеет значения. Важно лишь, сколько еще времени мы готовы ждать. Допустим, мы хотим оптимизировать время ожидания таким образом, чтобы оно не превышало 30 минут в 90% случаев. Тогда мы должны ждать максимум 11 минут, а потом отказаться от поездки на метро (это значение соответствует точке, в которой желтая кривая пересекает отметку 30 минут).
Можно провести аналогию с менеджментом проектов: чем дольше длится работа над проектом, тем больше дополнительного времени потребуется для его завершения. Любые уже затраченные ресурсы представляют собой «невозвратные затраты», следовательно, значение имеют лишь дополнительные ресурсы, необходимые для завершения проекта.
Безусловно, здесь нет никакой «магии». Существуют распределения, при которых ожидание является «инвестицией»: с каждой секундой ожидания дополнительное время ожидания уменьшается. Существует один вид распределения, при котором время ожидания не связано с дополнительным временем ожидания. Это распределение называется экспоненциальным (exponential distribution), а описанное его свойство называется «отсутствием памяти» (memorylessness). Также существуют распределения с «тяжелыми хвостами», при которых с каждой секундой ожидания дополнительное время ожидания возрастает. В случае Нью-Йоркского метро мы наблюдаем все эти варианты поведения в различных частях кривой.
Для тех, кто заинтересовался, весь код находится здесь!
